In an effort for transparency, I created this page to write about questions that are asked of me, and my response.
Didn’t Georgia already audit the machines?
They did some sort of audit. But, people dispute these audits are effective. For example, while these type of videos are making their way around the web, a significant portion of society will doubt the results of Georgia’s audit. My link is to a Trump tweet so you can see that Trump is pushing this himself, and this information is widely seen. I’m not trying to make a partisan statement by linking to Trump.
Here is a video of the same man succinctly explaining why he believes the Georgia recount was not valid.
Isn’t this just a partisan issue?
No. All sides believe in the importance of election integrity. For example, the NY Times, which is considered center or left, depending on your point of view, but not right, had this to say about Dominion in June of 2020.
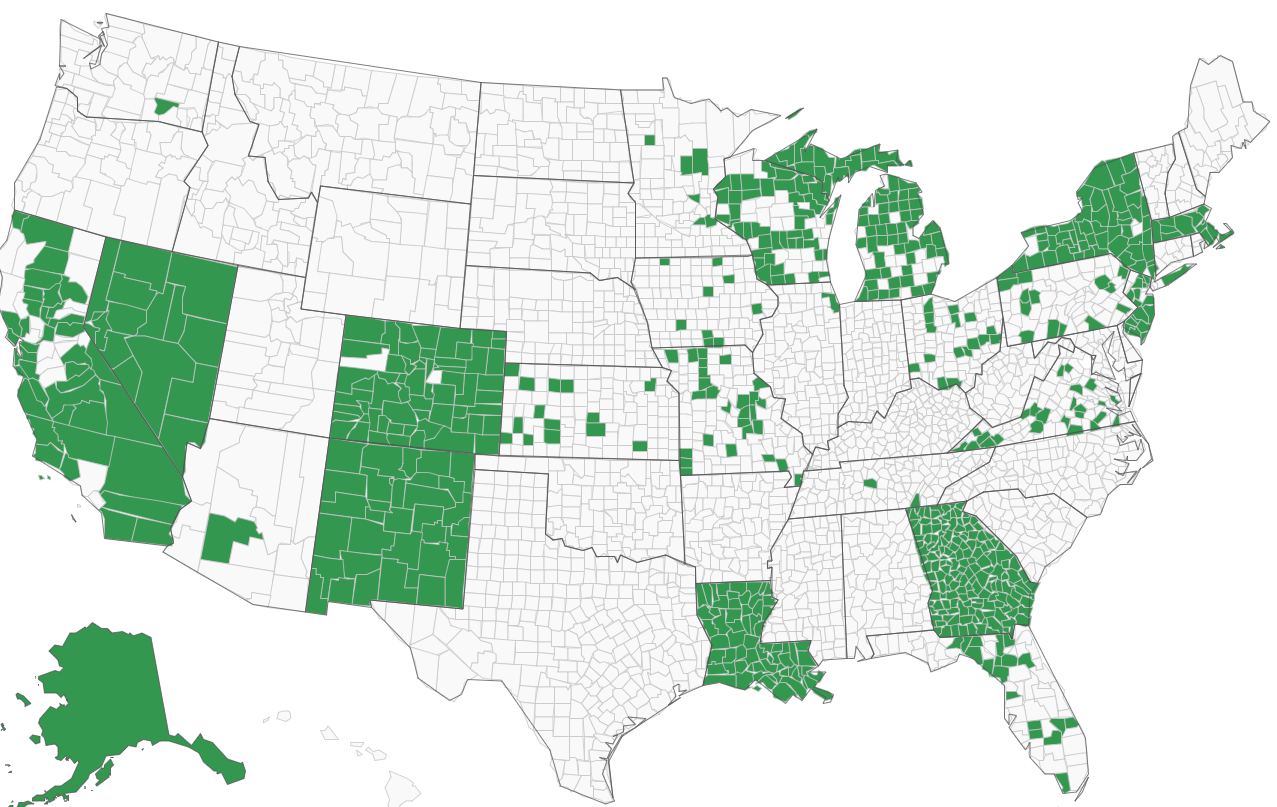
Are there really enough machines in Wisconsin to have changed the outcome there?
If you go to verifiedvoting.org, and selection Dominion, 2020, Wisconsin, and download the data, you’ll see that they are saying 527 precincts, 640,215 registered voters are on Dominion machines. The state only has a 20k vote difference among Biden and Trump. And, in my paper, the Dominion effect was calculated on a county basis, not precinct basis. To the extent counties are split on which machine they used, then my paper is underestimating the Dominion effect: the effect is likely bigger on a precinct by precinct basis; I don’t have the data to go to that detail.
But to answer the question: yes, based on published, public information, there are enough machines to change the election in Wisconsin.
Why don’t you show results for 2012 and 2016?
I did a fair amount of analysis on those election cycles with mixed results. It is challenging to tease out the effects. For example, suppose Dominion is deployed in 2012. Does it increase vote counts for Democrats in 2012, 2016 and 2020? Does it make the counts go up an additional increment each year? Are there years where the Dominion Effect is not in effect, so to speak, and the votes regress to what they should have been? It becomes harder to form a clear hypothesis when we mix the years. The hypothesis I posit in the paper is clear. I only test counties that had no Dominion in 2008 (by excluding New York) versus counties in 2020 that either did or did not have Dominion by that time.
Is it possible that there are pre-trends that can explain this result?
As I mentioned in the main article. I find the multivariable weighted least squares to be the most convincing. The reason for this is because the factor for Dominion by itself, when not controlled, does have pre-trends.
However, when using a weighted multivariate analysis, there is no pre-trend associated with the Dominion counties.
If you wish to see the two spreadsheets associated with this analysis, click here and here. If you wish to access a CSV file, click here.
If you wish to see how the data was constructed, click here here .
Are you sure that “Dominion” isn’t just a proxy for “Democratic Voter”?
We can test for this. The easiest way to test is to remove the Dominion flag for the 657 counties that have Dominion, and replace it with a flag for the top 657 most Democratic counties. This is performing the test assuming that a voting machine company had been adopted by the 657 most Democratic counties. Let’s call this company “MachinesForDems”. The model says that the “MachinesForDems Effect” is not the same as the Dominion Effect. The coefficient for “MachinesForDems” in the weighted model is -0.22% (not positive) and the two p–values are 0.07% (traditional) and 68.04% (robust–not significant).
We can do further tests by creating another flag, “MachinesForReps” which is the top 657 most Republican leaning counties. We can put all three flags into the model, Dominion, MachinesForDems, and MachinesForReps. Interestingly the “MachinesForReps” IS significant, and can be used as a control variable, but it doesn’t affect the significance of Dominion. Dominion’s coefficient for the weighted model is 1.56% and its p-values are 0.00% (traditional) and 0.09% (robust).
If you would like to see how I created this data, click here.
If you would like to see a spreadsheet with this analysis, click here .
Have you really accounted for very large and very small counties?
In our model, we are already using these adjustments:
- weighting by county size
- a field called “RuralUrbanContinuumCode2013”
These should adjust for county size, but in effort to address concerns of readers, I ran the model with two new flags:
- 657 counties with highest number of voters in 2008
- 657 counties with lowest number of voters in 2008
The Dominion Effect is still 1.55% and the p-values are 0.00% (traditional) 0.09% (robust). These p-values are suggesting less than 1 in 1000 chance of randomly occurring.
To further address this, I ran an additional model which also includes a field for the population per square mile. This model produces identical results of Dominion Effect of 1.55% and a p-value of 0.00% and 0.09%.
What about race? Why don’t you adjust for that?
We can do that too. To the model in the prior FAQ, I add a flag for the 657 counties that have the highest percentage of white-non-hispanic and another flag for the highest black-non-hispanic residences. This is as if a voting company somehow either got assigned to the highest percentage white or highest percentage black counties.
The Dominion Effect becomes 1.56% and the p-values are 0.00% and 0.15%.
Why don’t you adjust for age?
We can do that too. To the model used in the above FAQs, we can add a flag for the 657 counties with the highest percentage of residents over age 65 at the year 2010. At this point, I’d like to show the results of this enormous weighted-least squares.
| Variable | Coefficient | P-value | P-value Consistent |
| Intercept | -7.51% | 0.00% | 0.00% |
| RuralUrbanContinuumCode2013 | -0.31% | 0.00% | 0.28% |
| ManufacturingDependent2000 | -2.71% | 0.00% | 0.00% |
| HiAmenity | 0.23% | 23.48% | 65.86% |
| HiCreativeClass2000 | 5.29% | 0.00% | 0.00% |
| Low_Education_2015_update | 2.27% | 0.00% | 0.00% |
| PopChangeRate1019 | 0.17% | 1.77% | 0.00% |
| Net_International_Migration _Rate_2010_2019 | 0.14% | 0.10% | 55.07% |
| PopulationDensity | 0.00% | 88.32% | 96.33% |
| LargePopCountiesTop657 | 2.06% | 0.00% | 0.00% |
| SmallPopCountiesTop657 | 0.25% | 74.12% | 56.44% |
| HighDemPerTop657 | -0.60% | 0.22% | 23.64% |
| HighRepPerTop657 | 1.59% | 0.00% | 0.01% |
| OverAge65PercentTop657 | -3.84% | 0.00% | 0.00% |
| WhiteNonHispanicTop657 | -4.58% | 0.00% | 0.00% |
| BlackNonHispanicTop657 | 1.49% | 0.00% | 0.24% |
| Dominion | 1.42% | 0.00% | 0.24% |
This does slightly effect the Dominion Effect. It shrinks to 1.42% (a value that doesn’t change any conclusions in the main article) and the p-value remains significant at 0.00% (traditional) and 0.24% (robust).
If you would like to see an Excel workbook with this data and analysis, click here.
It should be noted, that if you run enough models, inevitable some will produce higher coefficients and some will produce lower coefficients, but the important fact here is that the coefficient remains in the 1.0 to 1.6% range discussed in the article and the p-value remains significant.
Why don’t you focus in changes in demographic trends over time?
We can do that too.
| Variable | Coefficient | P-value | P-value Consistent |
| Intercept | -6.6% | 0.00% | 0.00% |
| NetMigrationRate0010 | -0.1% | 0.00% | 0.00% |
| NetMigrationRate1019 | 0.3% | 0.00% | 0.00% |
| NaturalChangeRate0010 | 0.5% | 0.00% | 0.10% |
| NaturalChangeRate1019 | 0.3% | 0.10% | 11.20% |
| Immigration_Rate_2000_2010 | 0.2% | 0.00% | 10.10% |
| Net_International_Migration_Rate_2010_2019 | 0.3% | 0.00% | 32.00% |
| UnemployRate2007-UnEmployRate2019 | -1.0% | 0.00% | 0.00% |
| Dominion | 1.7% | 0.00% | 0.00% |
What does the above model look like if you add basic demographic info?
Like this:
| Variable | Coefficient | P-value | P-value Consistent |
| Intercept | 2.9% | 1.10% | 22.70% |
| NetMigrationRate0010 | -0.1% | 0.00% | 0.20% |
| NetMigrationRate1019 | 0.3% | 0.00% | 0.00% |
| NaturalChangeRate0010 | 0.7% | 0.00% | 0.00% |
| NaturalChangeRate1019 | -0.1% | 39.10% | 65.40% |
| Immigration_Rate_2000_2010 | 0.3% | 0.00% | 7.40% |
| Net_International_Migration_Rate_2010_2019 | 0.0% | 88.80% | 96.90% |
| UnemployRate2007-UnEmployRate2019 | -1.1% | 0.00% | 0.00% |
| PopDensity2010 | 0.0% | 0.00% | 25.70% |
| Under18Pct2010 | -0.3% | 0.00% | 0.80% |
| Age65AndOlderPct2010 | -0.3% | 0.00% | 0.00% |
| WhiteNonHispanicPct2010 | 0.0% | 39.40% | 71.20% |
| BlackNonHispanicPct2010 | 0.1% | 0.00% | 0.00% |
| Dominion | 1.5% | 0.00% | 0.40% |
Why don’t you test other machines?
Honestly, I was tired of working on this project and did not have flags for the other machines. However, someone who read this blog obtained flags, and I added them to the data. To the model shown in the above FAQ, I tested the various machines. Note, this was several different models, each testing the machines one at a time. When I put all of the machines at the same time into the model I encounter fitting problems.
Here are the results. Note each line is from its own model run. Dominion is the only significant machine. The Dominion “other” line is for “Sequoia (Dominion)” and “Premier/Diebold (Dominion)” machines. These machines are the most significant. Note that “20” indicates that the machine was used in 2020. For 2008, any machine could have been used, and it is too complicated to account for each permutation.
| Variable | Coefficient | P-value | P-value Consistent |
| Democracy.Live-20 | 0.1% | 56.8% | 80.7% |
| Dominion.other-20 | 3.0% | 0.0% | 0.0% |
| Dominion.Voting.Systems-20 | 1.5% | 0.0% | 0.3% |
| Election.Systems…Software-20 | 0.3% | 16.6% | 49.1% |
| Hart.InterCivic-20 | 0.0% | 98.4% | 99.2% |
| Other-20 | -0.1% | 74.6% | 89.3% |
If you wish to obtain an Excel workbook which shows how the above results were calculated, along with the results for the prior two FAQs, click here.
What other variables should we evaluate?
I recently reran this model against about 100 demographic variables. As noted above, some produce larger coefficients and others produce smaller. One issue I run into is that if you add enough variables, at some point the demographic variables start to be too correlated with each other and we have problems with multicollinearity. From a practical point of view what is occurring is many variables are describing the same thing and are overfitting. The most easy example to explain is the situation of a very largely populated county. From a demographic point of view, these counties simultaneously have large groups of very educated people and also large groups of very uneducated people. They also have very high income people and very low income people. They also have a high percentage of very young people. So, if you put the variables of size of county, high education, low education, high income, low income, and very young people in the same models, these variables are competing with each other to flag the very large cities. This can cause overfit issues and multicollinearity issues which can render the models less reliable. I think the best thing for me to say about this is it appears that the Dominion Effect, if real is somewhere between 1.0% and 1.6%. The p-values are typically significant. Only a full forensic audit would reveal the true nature of the situation.
Are you sure the model isn’t just picking up state specific effects?
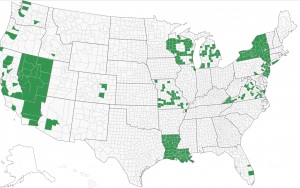
Someone suggested that I delete all states except for states that are split with some counties having Dominion and other counties in the state not using Dominion. These split states are: Arizona, California, Colorado, Florida, Illinois, Iowa, Kansas, Massachusetts, Michigan, Minnesota, Missouri, Nevada, New Jersey, Ohio, Pennsylvania, Tennessee, Virginia, Washington, and Wisconsin.
Using the original model, and only including these split states, the Dominion Effect in the weighted model is 1.54%. The power of the model is diminished slightly with so many fewer counties. The p-values for the weighted model are 0.00% (traditional) and 1.20% (robust).
This suggests that when we run the model only on split county states, the Dominion Effect remains.
If you would like to see an excel workbook with this analysis, click here .
If you would like to see how the voting size and partisan share fields are created, click here.
In your analysis, if you remove Georgia, the Dominion Effect is greatly diminished? Doesn’t this invalidate your work?
Not really. The results are still valid. They Dominion coefficient using unweighted values is 0.43% with p-values 14.63% (traditional) and 12.74% (robust) and for weighted values they are 0.96% with p-values of 0.00% (traditional) and 6.05% (robust). I believe this is indicating that Georgia is the strongest case for auditing. Because the unweighted coefficients become much lower without Georgia, to me this is saying that Georgia is a prime candidate for testing small counties; the Dominion effect is likely strong there. Because the coefficient stays relatively high for weighted, it seems to say that the “Dominion Effect” is stronger in big cities outside of Georgia but not as strong in small counties. Click here for an excel workbook showing results without Georgia.
I am doing heavy analysis and encountering modeling errors? Is there a problem with the data?
Yes. Many people have analyzed the data and one valid criticism has occurred. There are five data points that have incorrect demographic data. If you do heavy demographic modeling, I recommend you remove these five data points: “Baltimore city”, “Saint Louis”, “St. Louis city”, “Carson City”, “Dona Ana”.
Why are there older versions of this article on the web?
I wrote and updated this article by posting it on the web and sharing it with other statistical analysts. I did this prior to allowing it to be shared on social media. There were actually four different versions of this analysis. Version 3 had a data error in the denominator of the Y variable which over-emphasized the coefficients. A reviewer caught that, and it was fixed before this article was widely shared on social media. If you come across older cached versions of this article, just know they were pre-release drafts.
Furthermore, upon recently reviewing about 100 demographic variables, I think it is safer to say the Dominion Effect is somewhere between 1.0% and 1.6% instead of just saying 1.5%.
What are the biggest challenges to your model?
I have disclosed the biggest challenges in the FAQ above. I think the biggest issue is people wonder if I have proven causality. All I can say is, I am attempting to address any concerns people have about that in the FAQ above. It is very possible that some third factor is causing the results we are seeing, and it is not the Dominion machines. I have attempted to mitigate these concerns by controlling for other factors and disclosing pre-trend issues. My main point is, I’ve shown plausible data. Why resist audits that prove to the world there is nothing to see here?