Written by Benjamin Turner
This article was published on 10/9/202 on 7:15 am on LinkedIn. It was removed on 9:15 am of the same day by LinkedIn.
Fraudspotters, LLC, nor its employees express any opinion about this article. We are publishing it out of solidarity with an employee.
As an actuary, I’m asked how long to expect Joe Biden to live.
This is a morbid question but relevant. We just experienced a VP debate which may have actually been our presidential debate, and this is a good opportunity to teach people about actuarial mathematics. And, as an actuary, this type of stuff is literally what I do, so it is not morbid to me; it is common place.
So, without further ado…
To calculate the mortality rate go to a published actuary table. An obvious one is found here, and I will reference this table. You should see a webpage that looks like the image below. This is a table produced by the Social Security Administration to project how long people will live for purposes of understanding how much will be paid from Social Security (at a younger age, I worked as a pension actuarial analyst for Mercer Consulting).
The place that says “select a year for period life table: 2016” is referencing the data / time period used for estimation. We are going to use 2016 as this is the latest year offered at this website; however, if you select slightly different years you won’t see much of a change as the mortality rate is not changing much for Americans.
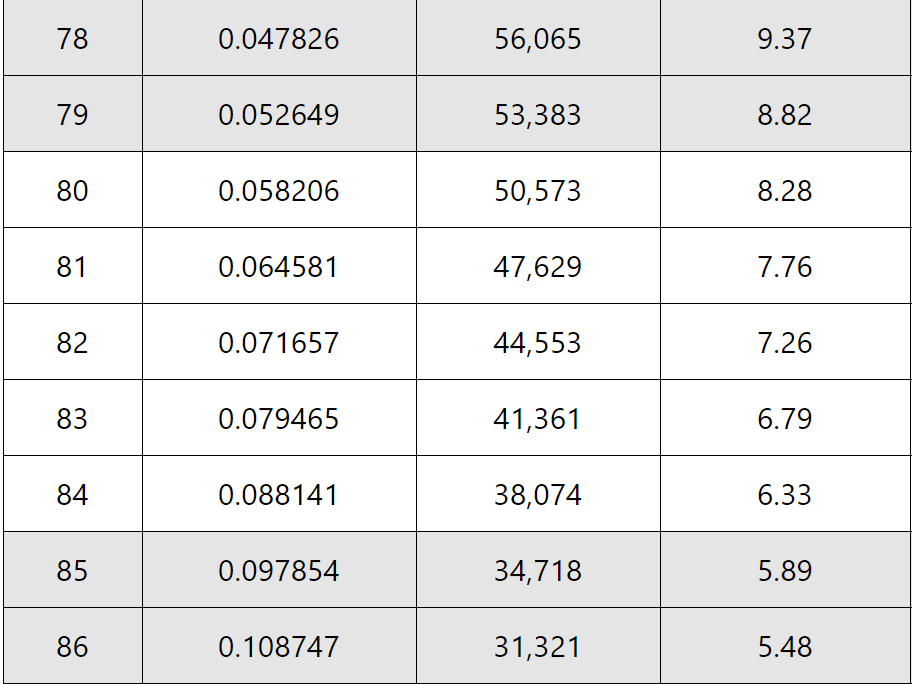
Since Joe Biden is male and will be 78 in November, we are going to obtain data relevant to that age and gender. Below is the data I will be using. In the first column, the first value, which is .047826, is the chance of dying in that age. I will be focused on this column because if we do 1-X on this column we get the survival rate. So, for example, the chance of surviving from age 78 to age 79 is 1-.047826 = 0.952174 = 95.2174% This is similar to the chance of surviving Covid-19 if you are over 70, which is 94.6%.
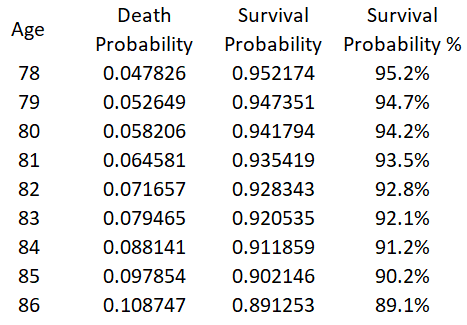
If we perform the 1-X calculation on all of the relevant ages we obtain the following table shown below. The survival probability is the chance of living to the next age, given that you survived to the given age. So, for example, if Joe Biden lives to age 86 he has an 89.1% chance of making it to age 87.
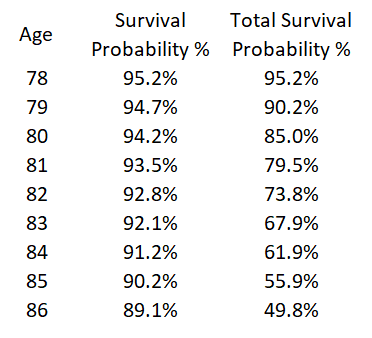
If we want to calculate the chance of making it several years than we combine the survival rates by multiplying them together. For example, the chance of making it from age 78 through age 79 to age 80 is 95.2% X 94.7% = 90.2%
If we perform this type of mathematics from age to age, we obtain Joe Biden’s chances of making it to a given age. As the table below shows, if Joe Biden serves two terms, his expected chance of surviving to the end is 49.8%. In other words, over a two-term time period, there is a 50.2% chance that Joe Biden’s VP has to be sworn-in. In addition to mortality, there is the chance of becoming disabled, but that is not the purpose of this post.
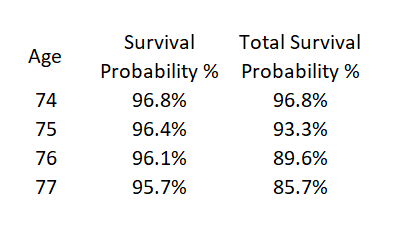
If you have read this far, you probably are wondering Donald Trump’s chances of making it to the end of four years. Donald Trump is male and turned 74 back in June, so we’ll use male and age 74. As the table below shows, there is a 85.7% chance of survival. In other words, there is 14.3% chance that over the next term, Donald Trump’s VP would need to be sworn- in. (Please note, the purpose of this article is not to compare/contrast Donald Trump’s chance of survival to that of Joe Biden. There are other factors besides their ages that affect their probability of survival. I am not a privy to those factors. This article is to teach the reader the basic concepts of how to calculate the chances of survival.)
Final thoughts/changing topics.
LinkedIn censored my last article about the mortality rate of infectious diseases on the grounds of “misinformation”. They removed it. When I challenged their removal, they gave a “second look” and affirmed their ban of my article. All data in that article was from the reputable sources such as the CDC or the Social Security Administration; I provided no original research. My only contribution was that I simply explained to the reader how to do the math, like I am doing in this article. That article can be seen here.
To LinkedIn, I’d like to coin a phrase by saying the following, “True science never censors, it only counters with the truth.” If you believe something I say is untrue, please counter with something you believe is true.

